Начисление процентов — одна из основных операций в экономике и инвестировании. Самый близкий всем пример — депозит в банке, где вложенные деньги в конце периода возвращаются к владельцу с прибылью.
А что будет, если повторить этот цикл несколько раз? Тут то и появляется понятие простых и сложных процентов, которым посвящена эта статья.
- Простые и сложные проценты
- Формулы сложных процентов по вкладам и примеры решения задач
- Калькулятор сложных процентов от Вебинвеста
- Формула сложных процентов по вкладам
- Простые проценты
- Сложные проценты
- Как выбрать лучшие условия?
- Простые и сложные проценты в инвестициях — формулы и примеры
- 1. Сложные проценты — что это такое, формула расчета
- 2. Примеры сложных процентов в инвестициях
- 2.1. Пример: инвестируем ежемесячно в банк под 8% (срок 10 лет)
- 2.2. Пример: инвестируем в банк под 8% (срок 20 лет)
- 2.3. Пример: инвестируем в ценные бумаги под 12% (срок 20 лет)
- Финансовая грамотность | 7.5.1. Способы начисления процентов. Простые и сложные проценты
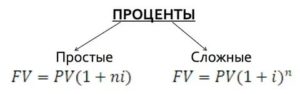
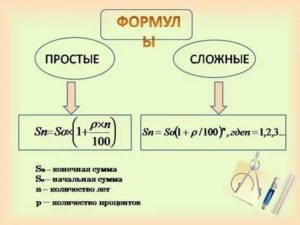
- Формула простых процентов:
- Формула сложных процентов:
- Формула простых и сложных процентов: как это работает
- Что такое сложный процент?
- Примеры расчета простого и сложного процента
- Простой
- Сложный
- Подробнее о сложном проценте
- Задача №1
- Задача №2
- Выводы
- Пример расчета с реальным банковским вкладом
- Пример расчета на большом отрезке времени
- Как поможет сложный процент в построении капитала?
- Вспомогательные формулы
- Заключение
- Простые и сложные проценты
- Дисконтирование и учет по простым процентным ставкам
- Определение срока ссуды и величины простой процентной ставки
- Определение срока платежа и сложных процентных ставок
- Потоки платежей. Постоянные финансовые ренты
- Обобщенные параметры потоков платежей
- Годовая рента
- Определение срока ренты
- 💡 Видео
Простые и сложные проценты
Инвесторы, которые работают на рынке Форекс, сталкиваются с повторным вложением денег (реинвестированием) постоянно. Если банковские депозиты приносят владельцам прибыль через несколько месяцев или даже год, то на валютном рынке прибыль/убыток появляется после каждой сделки.
Поэтому все, кто интересуется инвестициями на Форексе, будут регулярно работать с простыми и сложными процентами. Давайте же разберемся, что же означают эти понятия.
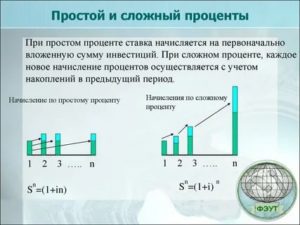
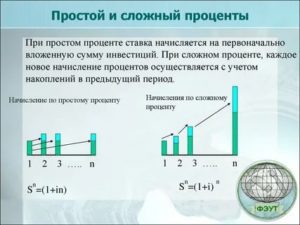
Простой процент — прибыль по многоразовым вкладам за каждый период времени всегда начисляется только на первоначальную сумму.
Пример: депозит 5000$ под 20% годовых. По схеме простого процента и в первый, и во второй, и в любой другой год прибыль составит 1000$. Чтобы узнать прибыль за N лет, просто умножьте прибыль за один год на число N.
Простой процент используется в случаях, когда база начисления процентов всегда равна начальной сумме вложений. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты по многоразовым вкладам за каждый период начисляются на первоначальную сумму и всю полученную до этого прибыль.
Пример: депозит 5000$ под 20% годовых. В первый год прибыль составит 5000$ * 20% = 1000$, во второй (5000$ + 1000$) * 20% = 1200$, в третий (5000$ +1000$ + 1200$) * 20% = 1440$ и так далее.
Каждый раз, когда инвестор хочет несколько раз «прокрутить» свои деньги через инвестиционный инструмент, он сталкивается со сложным процентом. Полученная прибыль на первом круге реинвестируется и проценты уже начисляются на более крупную сумму.
В инвестициях на рынке Форекс сложный процент используется постоянно, потому что сумма вложений меняется после каждой сделки. Многие инвесторы используют тактику «вложил и забыл», оставляя полученную прибыль работать вместе со стартовым вкладом.
Разница между простыми и сложными процентами на первый взгляд кажется не такой уж большой. Но чем больше проходит времени, тем очевиднее становится преимущество сложных процентов:
Простые и сложные проценты на одном графике
Конечно, это всё теория и на практике добиться 30-кратного реинвестирования прибыли совсем непросто. Но факт остаётся фактом — сложные проценты могут сослужить хорошую службу инвестору. И чтобы умело их использовать, нужно правильно их считать, в чём помогут несколько полезных формул.
↑ К СОДЕРЖАНИЮ ↑
Формулы сложных процентов по вкладам и примеры решения задач
Формулы сложных процентов в математике встречаются постоянно, особенно если речь идёт об экономических задачах. Представьте, что вам нужно рассчитать прибыль от банковского вклада за несколько лет. Для этого понадобится такая информация:
- начальная сумма вклада (K нулевая или К0)
- ставка доходности (R) — переводится из процентов в число (10% = 0.1)
- количество периодов реинвестирования, то есть лет (n)
А конечную сумму вклада мы назовем просто K. Её можно рассчитать по формуле:
Конечная сумма при расчёте сложных процентов по вкладу
Пример задачи: Инвестор П. положил на депозит в банке 10000$ под 10% годовых. Какую прибыль он получит через 5 лет?
Для начала, давайте узнаем конечную сумму вклада по формуле:
K = 10000$ * (1 + 0.1)5 = 16105.1$
Прибыль (P) — это разница между конечной и стартовой суммой вклада. Считаем:
P = K — К0 = 16105.1$ — 10000$ = 6105.1$
Можно даже подсчитать прибыль в процентах, для этого нужно найти не разницу, а отношение между конечной и стартовой суммой:
P (%) = K/К0 — 1 = 16105.1$ / 10000$— 1= 61.05%
Используя формулу сложных процентов, вы всегда можете предсказать результат инвестирования в будущем. Впрочем, бывают ситуации, когда вам нужно узнать не конечную, а стартовую сумму вклада. Её можно найти по той же формуле сложных процентов по вкладам, но надо немного её изменить:
Формула расчёта сложных процентов для поиска стартовой суммы вклада
Пример задачи: Инвестор В. хочет узнать, сколько ему надо вложить рублей под 20% годовых сейчас, чтобы через 3 года стать рублёвым миллионером.
Используем формулу:
К0 = 1000000₽ / (1 + 0.2)3 = 578703.7₽
Кроме суммы вклада, через формулу можно найти и остальные параметры. Например, зная стартовую и конечную сумму, можно узнать процентную ставку или количество периодов реинвестирования.
https://www.youtube.com/watch?v=H-wc9le5aAw
Начнем с процентной ставки:
Формула расчёта сложных процентов по вкладу для поиска нужной процентной ставки
Пример задачи: Инвестор Р. хочет выяснить, вклад с какой процентной ставкой ему нужен, чтобы заработать 10000$ за 3 года, изначально вложив 20000$.
Для начала нужно посчитать конечную сумму, так как мы знаем только прибыль:
K = К0 + P = 20000$ + 10000$ = 30000$
А теперь можно использовать формулу:
R = (30000$ / 20000$) 1/3 — 1 = 14.47%
Чтобы получить такую доходность, банковский депозит не подойдёт, а вот консервативный ПАММ-счёт — вполне.
Напоследок давайте выясним, как рассчитать, на какой срок нужно положить деньги, чтобы получить нужную нам прибыль. Без логарифмов не обойтись:
Расчёт сложных процентов по вкладу — поиск нужного количества периодов реинвестирования
Пример задачи: сколько лет нужно держать деньги на депозите в банке под 25% годовых, чтобы 50000 рублей превратить в 100000?
Подставляем в формулу:
n = log1+0.25 100000/50000 = 3.11 лет
Кстати, если речь идёт о банке, то 3.11 лет округляются до 4 — вы обычно не можете снять свои деньги до окончания периода действия вклада. Условия конкретного инвестиционного инструмента всегда стоит учитывать при решении подобных задач.
Кроме рассмотренных нами задач существуют и более сложные. Например, довольно распространённая история — у инвестора есть вклад с возможностью пополнения. Часть каждой зарплаты отправляется туда и надо выяснить, какой же будет результат по итогам.
Пример задачи: Инвестор З. вложил 1000$ и откладывает 50$ каждый месяц. Процентная ставка — 1% в месяц. Какая сумма накопится через 5 лет?
Чтобы узнать результат, нужно создать табличку:
Расчёт результатов инвестирования с доливками, с учётом сложных процентов
В первый месяц сумма инвестиций составила 1000$, на неё начислен 1% — итого 1010$. Во второй месяц работают уже 1010$ и еще 50$, которые инвестор внёс дополнительно. Итого — 1070.10. И так далее…
Разумеется, считать эти таблички каждый раз — довольно напряжно, решать логарифмы — тем более. Поэтому специально для вас при помощи программы Microsoft Excel я сделал небольшой файлик для решения задач по сложным процентам.
↑ К СОДЕРЖАНИЮ ↑
Калькулятор сложных процентов от Вебинвеста
Многие формулы сложных процентов в математике на обычном калькуляторе не посчитаешь — нужно использовать специальные программы или сайты. Microsoft Excel позволяет делать практически любые прикладные расчёты быстро и удобно — всего-то нужно скачать файл и работать с ним.
По формулам из статьи я сделал небольшой калькулятор для расчёта сложных процентов. Вот так выглядит одна из страниц:
Скриншот из калькулятора сложных процентов с капитализацией.
С помощью файла вы сможете решить задачи, которые мы рассматривали по ходу статьи:
- расчёт конечной суммы вклада;
- расчёт начальной суммы вклада;
- расчёт нужной процентной ставки;
- расчёт срока инвестирования;
- расчёт конечной суммы вклада с учётом добавочных вложений или снятия прибыли.
Как получить калькулятор сложных процентов от Вебинвеста? Очень легко — воспользуйтесь формой ниже:
Больше подробностей о калькуляторе сложных процентов вы можете узнать на этой странице.
↑ К СОДЕРЖАНИЮ ↑
Ну что, ощутили магию сложных процентов? Если да, поделитесь статьёй в соцсетях, пусть ваши друзья тоже её почувствуют 🙂
Удачи и терпения в инвестициях!
Видео:Сложный процент | Что такое сложные проценты простыми словами, формула и расчёт сложных процентовСкачать

Формула сложных процентов по вкладам
Любой клиент, выбирая банк для вложения своего капитала, обращает внимание не только на надежность финансового учреждения, но и на процентную ставку, для получения максимального дохода по вкладу.
Однако, необходимо учитывать не столько годовую ставку, сколько принцип начисления прибыли. В сфере финансов есть два метода: простой и сложный процент.
Нужно ознакомиться с формулами и основными параметрами расчетов для понимания, какое из предложений по вкладам будет наиболее выгодным для клиента, при различных условиях заключения договора.
- 1 Простые проценты
- 2 Сложные проценты
- 3 Как выбрать лучшие условия?
Простые проценты
Простой процент означает, что начисление дополнительного дохода происходит единоразово по окончании периода хранения средств. При этом, если действие депозитного договора автоматически продляется, доход за следующий период будет начисляться на первоначальную сумму взноса, без учета процентов за прошлый срок.
https://www.youtube.com/watch?v=clfh5n86VJ8
Простой процент начисляется по формуле:
S= V*(1+P*n/100),
где S – сумма, которую получит клиент по окончании срока действия депозита (первоначальный вклад + начисленный процент),
V – первоначальная сумма вложения,
P – процентная ставка за период,
n – период вложения.
При открытии депозита на 1 год в размере 100 тыс. рублей и 8 % годовых, клиент через год получит 100*(1+8*1/100)=108 тыс. рублей.
- При продлении договора еще на год, по истечении данного периода вкладчик получит такой же доход в 8 тыс. рублей и заберет сумму в 116 тыс.
- Если размещение вклада по договору происходит на короткий период (несколько месяцев), то годовую процентную ставку нужно разделить на 12 месяцев и умножить на период вложения.
- При вложении на полгода вкладчик получит: 100*(1+8/12*6/100) = 104 тыс. рублей.
Сложные проценты
Начисление сложных процентов по депозиту или капитализация – это эффект, при котором процент начисления прибавляется к первоначальной сумме вклада, а на эту сумму вновь происходит начисление процента в следующий период.
Капитализация происходит с разной периодичностью (каждый месяц, раз в полгода и т.п.)
Расчет в этом случае производится по формуле:
S= V*(1+P/100)n,
n в данном случае – количество периодов капитализации.
Например, при годовой сделке на сумму 100 тыс. рублей и 8% за год и ежемесячном начислении процентов, получится:
100*(1+8/100/12)12 = 108,3 тыс. рублей.
- Наглядно видно, что дополнительный доход с учетом капитализации больше, чем получаемый по формуле простого процента.
- Но при выборе лучшего предложения по оформлению вклада с капитализацией, нужно уточнить периодичность начисления процентов. Чем чаще это будет происходить, тем большая сумма получится при закрытии депозитного счета.
Как выбрать лучшие условия?
Начисление простых процентов происходит в арифметической прогрессии, в то время как сложные проценты выдают прибыль в прогрессии геометрической.
Это не означает, что для успешного вложения всегда стоит останавливать свой выбор на предложении с капитализацией вклада.
С учетом срока действия депозитного договора, суммы вклада, и (что самое основное) периодичности начисления процентов, не всегда прибыль от капитализации будет больше, чем при заключении договора с одноразовой выплатой процентов в конце периода.
- При заключении договора на 3 месяца и периодичности капитализации в 6 месяцев, клиент заберет свой вклад раньше, чем произойдет начисление процентов. В этом случае оформление простого вклада будет иметь более логичный смысл.
- Также, если есть возможность выбора частоты начисления процентов (каждую неделю, месяц или три месяца), лучше выбрать капитализацию, где проценты будут приходить на счет в более короткие термины. Выбирая между периодичностью начислений в три месяца и один, примите решение в пользу последнего.
- При открытии краткосрочного вклада, клиентам банка нужно учесть, что на день закрытия депозита начисление процентов не происходит. Если вкладчик оформил договор на 2 недели и забирает средства на 14-й день, то начисление процентов будет произведено только за 13 дней.
В тексте депозитного договора буквально не говорится, будет происходить начисление простых или сложных процентов. Поэтому, исходя из условий договора, клиент сам должен понять, о чем идет речь.
Основное отличие:
- Если процент начисляется один раз по окончании срока действия депозита, расчет будет произведен по простой формуле.
- Если указана частота начисления процентов, вы имеете дело с капитализацией.
Самое выгодное для вкладчика:
- депозит с капитализацией,
- ежемесячное начисление процентов,
- возможность пополнения счета.
По таким вкладам, правда, у банков редко бывают высокие процентные ставки. Но здесь уже каждый клиент должен сам искать более выгодное решение.
Видео:ФОРМУЛЫ СЛОЖНЫХ И ПРОСТЫХ ПРОЦЕНТОВСкачать

Простые и сложные проценты в инвестициях — формулы и примеры
В этой статье мы рассмотрим математический вопрос, который играет большую роль в инвестициях: влияние простых и сложных процентов на итоговый результат. Приведём формулы и примеры для расчётов.
Принципы сложных процентов прежде всего будет опираться на действия с деньгами. Поэтому все примеры приведены именно в ключе для инвесторов.
Давайте рассмотрим на реальных примерах с цифрами как работают сложные проценты, чтобы более точно понимать их преимущества, а уже сразу после этого перейдем к описанию вариантов для инвестирования.
1. Сложные проценты — что это такое, формула расчета
Сложный процент — это начисление процентов на уже выплаченные суммы. На большом промежутке времени происходит лавинообразное приращение.
Для обычных граждан самым простым примером является банковский вклад. Если деньги пролежали год на депозите, то на следующий год сумма будет уже больше, поэтому и доход будет выше. И так каждый год.
Формула сложных процентов:
Где
- Dohod – будущая стоимость (конечный результат);
- D – первоначальная сумма инвестиции;
- S – годовая процентная ставка;
- K – частота капитализации (сколько раз в году выплачивается сумма);
- n – количество лет, для которого производится расчет
Формулу сложных процентов с ежемесячным пополнением:Dohod = D × (1 + S/K)N×K + [ sum_popolnenie×((1+ S/K)N×K — 1 ] / (S/K)
Где
- sum_popolnenie – сумма ежемесячного пополнения;
Альберт Эйнштейн назвал сложные проценты самым важным изобретением человечества.
Если ставка одинаковая из года в год, а пополнение происходит один раз в год, то можно вручную быстро рассчитать итоговый доход. Рассчитаем сложные проценты для процентной ставки 10% годовых из года в год:
первый год: 110%второй год: 121% (1.1 × 1.1)третий год: 133.1% (1.1 × 1.1 × 1.1)и т.д.
Закономерность понятна. Надо просто перемножить количество лет на ставку 1.
1 (10%) и сразу получим итоговый доход. К примеру, если бы мы положили сумму 100 тыс. на три года под 10% и каждый раз капитализировали проценты, то в конце трёх лет сумма увеличилась до 133.1 тыс.
Без капитализации было бы 130 тыс.
https://www.youtube.com/watch?v=VHEFGoz2zew
Простые проценты начисляются просто путем добавления к сумме инвестирования (без капитализации). Чтобы рассчитать свой доход нужно просто умножить число лет на годовую доходность.
2. Примеры сложных процентов в инвестициях
Можно смело сказать, что каждый рубль отложенный сегодня принесёт десятки рублей через 10 лет за счёт постоянного реинвестирования прибыли. Подобным образом разбогатели многие миллиардеры (Уоррен Баффет).
Мое богатство — это результат комбинации нескольких факторов жизни в США, хороших генов и аккумулирующего эффекта сложных процентов.
Уоррен Баффет Кривые доходности при сложных и простых процентах
Обратите внимание, что эффект заметен со временем все сильнее и в конце кривая сложных процентов приобретает экспоненциальный характер, в то время как простые проценты растут линейно. Рассмотрим на конкретных примерах этот принцип.
2.1. Пример: инвестируем ежемесячно в банк под 8% (срок 10 лет)
Если откладывать ежемесячно по 10 тысяч рублей «под подушку» или просто на банковский счёт, то через 10 лет (120 месяцев) сумма будет 1.2 млн рублей (120 умножаем на 10 тыс).
Если же откладывать эти деньги на банковский вклад под 8% годовых, то сумма по истечению 10 лет будет значительно больше 1 851 738 рублей. Чистый доход от процентов 641 738 рублей (чуть больше 50% за все время).
Новички по ошибке могут получить неправильную сумму, если просто прибавить 8% к отложенной сумме, но это неверно.
Сложный процент можно посчитать лишь на онлайн калькуляторе или самостоятельно с помощью длительных вычислений.
Расчёты на калькуляторе сложных процентов:
Выписка по балансу:
Примечание
В некоторые периоды можно найти ставку на вкладах гораздо выше 8% и доход был бы в таком случае был заметно больше.
2.2. Пример: инвестируем в банк под 8% (срок 20 лет)
Теперь увеличим срок нашего инвестирования с 10 лет до 20 лет. Мы будем также откладывать по 10 тысяч рублей и всю полученную прибыль реинвестировать. Теперь по истечению срока сумма будет 5 938 760 рублей вместо 2 400 000. Чистый доход от процентов 3 528 760. Эта сумма больше всех суммарных вложений в 1.5 раза (150% прибыли за все время)!
Это наглядный пример того, что чем больший период мы рассматриваем, тем заметнее будет действие сложных процентов.
2.3. Пример: инвестируем в ценные бумаги под 12% (срок 20 лет)
Последний пример депозита в инвестиции. Откладываем по 10 тысяч рублей ежемесячно на протяжении 20 лет, но теперь мы инвестируем деньги в акции и небольшую часть в облигации. Как показала реальная история, такой инвестиционный портфель в среднем за год приносит 12% с учетом дивидендов от акций при самой простой стратегии «купи и держи».
Итого, сумма на конец срока: 9 999 681 рублей. Чистый доход 7 589 681 рублей.
И это не результат везения, не фантастика, а очень реальные цифры дохода, которые доступны каждому лицу! По факту можно даже получить и больше и даже за более короткий срок, если выйти с рынка на его пике, а докупиться в конце цикла падения, но для подобных «маневров» необходимы основы трейдинга и немного времени на совершение торговых операций.
Хочу подчеркнуть, что мы рассмотрели реальные варианты без каких-либо везений и прочее. Такого результата добьется каждый, кто просто вложит в ценные бумаги и не будет дергаться и пытаться что-то еще сделать. Такая стратегия называется: купи и держи.
Примечание
При инвестировании в зарубежные акции доход был бы еще больше (где-то в два раза), поскольку по статистике рубль обесценивается к доллару примерно на 100% каждые 20 лет.
Также важно откладывать в начале как можно больше. Это сильно повышает будущую доходность.
Теперь, понимая силу сложных процентов, поговорим о том, во что лучше всего вложить деньги, чтобы получать пассивный доход. Какие конкретно варианты инвестирования существуют, каковы их риски и преимущества можно прочитать:
Смотрите также видео про сложные проценты:
Видео:Формула сложных процентовСкачать

Финансовая грамотность | 7.5.1. Способы начисления процентов. Простые и сложные проценты
В зависимости от того, у кого вы взяли кредит (заём), на какую сумму и на какой срок, у вас могут быть разные способы начисления процентов, графики платежей, сопутствующие комиссии, штрафы и пени в случае просрочки.
Проценты могут начисляться в конце срока кредита или периодически, до окончания срока. При начислении промежуточных процентов возможны следующие варианты:
- проценты сразу выплачиваются кредитору и не увеличивают сумму долга;
- проценты присоединяются к сумме долга (капитализация процентов), и следующее начисление производится уже на возросшую сумму долга с учетом предыдущих процентов, – тогда можно говорить о «сложных процентах» (впрочем, в потребительском кредитовании, согласно пункту 2 статьи 317.1 ГК РФ, сложные проценты использоваться не должны);
- проценты отражаются в учете кредитора как причитающиеся ему, но следующее начисление процентов производится только на первоначальную сумму долга, – тогда говорят о «простых процентах».
Формула простых процентов:
,
где — сумма долга, — сумма долга с процентами, r — ставка процента за период (обычно за 1 год, но могут использоваться и другие периоды), n — число периодов начисления.
Если ставка выражена в годовых процентах, а проценты надо рассчитать за период меньше чем год, то при использовании формулы простых процентов необходимо разделить годовую ставку на количество дней в году (обычно 365 или 366, но иногда используется и условная величина 360 дней) и умножить на фактическое количество дней пользования заемными средствами, начиная со дня, следующего за днем получения средств:
,
где — сумма долга, — сумма долга с процентами, r — годовая ставка процента, m — фактическое количество дней пользования заемными средствами.
Формула сложных процентов:
где — сумма долга, — сумма долга с процентами, r — ставка процента за один период (опять-таки обычно за 1 год, но могут использоваться и другие периоды), n — число периодов начисления.
Если ставка выражена в годовых процентах, а проценты надо рассчитать за период меньше чем год, то при использовании формулы сложных процентов необходимо найти условную однодневную ставку, для чего из величины (1+ r/100) извлекается корень 365 или 366 степени.
А потом эта величина возводится в степень, соответствующую фактическому количеству дней пользования заемными средствами (понятно, что это можно сделать только с использованием вычислительной техники).
Тогда формула будет выглядеть следующим образом:
где — сумма долга, — сумма долга с процентами, r — годовая ставка процента, m — фактическое количество дней пользования заемными средствами.
Сложные проценты сложнее для расчетов (что было особенно значимо до изобретения вычислительной техники), но на длительных промежутках времени они экономически более справедливы.
Ведь если заемщик должен банку проценты, но не выплатил их, значит, он пользуется как первоначальным долгом, так и суммой процентов. Поэтому справедливо начислять проценты за следующие периоды на возросшую сумму, а не только на первоначальный долг.
Особенно явно это проявляется для долгосрочных кредитов со сроком более одного года. Примеры с расчетами приведены ниже.
Пример 2а. Марина Ежикова 01.04.2014 г. взяла заём у соседки Людмилы на сумму 50 000 рублей сроком на 3 года, ставка 10% годовых, проценты простые, погашение займа вместе с процентами в конце срока. Какую сумму выплатит Марина при погашении займа?
Пример 2б. Капитолина Дикобразова взяла заём у соседки Светланы на сумму 50 000 рублей сроком на 3 года, ставка 10% годовых, проценты сложные, погашение займа вместе с процентами в конце срока. Какую сумму выплатит Марина при погашении займа?
Решение:
Как видно, сложные проценты принесли займодавцу лишние 1550 рублей. За три года немного, но все же сумма процентов у Светланы получилась на 1/10 больше, чем у Людмилы.
Ситуация меняется на противоположную, если срок кредита или займа короткий — меньше одного года: тут при одинаковой ставке заемщик заплатит по сложным процентам меньше, чем по простым.
Пример 3а. Индивидуальный предприниматель Елисей 01.04.2017 г.
взял кредит на сумму 150 000 рублей сроком на 1 год, ставка 25% годовых, проценты выплачиваются ежемесячно без погашения основной суммы долга (поскольку банк начисляет проценты ежедневно и не указано иное, значит, проценты уплачиваются по простой ставке). Какую сумму уплатит Елисей за первые 3 месяца?
Решение: в первых 3 месяцах указанного периода 91 день, поэтому Елисей уплатит
Пример 3б. Индивидуальный предприниматель Дорофей 01.04.2017 г. взял кредит на сумму 150 000 рублей сроком на 1 год, ставка 25% годовых, проценты выплачиваются ежеквартально, начисление производится по сложной ставке. Какую сумму уплатит Дорофей за первые 3 месяца?
Решение: опять-таки в первых 3 месяцах указанного периода 91 день, поэтому Дорофей уплатит
Как видно, Дорофей заплатит меньше, чем Елисей.
Итак, сложные проценты выгоднее для кредитора на длинном горизонте — больше одного года: тогда при одной и той же годовой процентной ставке должник по формуле сложных процентов заплатит больше, чем по формуле простых процентов. А на периодах меньше года, наоборот, сложные проценты выгоднее должнику, чем простые, если ставка выражена в процентах годовых.
Все расчеты такого рода, конечно, удобно делать не вручную, а с помощью компьютерных программ, например, всем известного Excel.
Видео:Расчет сложных процентов (4 примера)Скачать

Формула простых и сложных процентов: как это работает
Данная тема относится к основам финансовой грамотности и обязательна для изучения при инвестировании, построении капитала или просто для накопления необходимой суммы денег.
В финансовой сфере принято отличать принцип расчета простых и сложных процентов. Например, в банковской сфере сложный процент понимается под понятием капитализации. А в инвестициях часто используют слово «реинвестирование».
Что такое сложный процент?
Сложным процентом называют геометрическую прогрессию денежной суммы, при которой начисленные проценты прибыли прибавляются к базовой сумме, в следующем периоде базовая сумма увеличивается и процент начисляется уже на нее. За счет этого эффекта доходность получается выше, чем при простом проценте.
Капитализация или реинвестирование — это суммирование начисляемых процентов с базовой суммой в обозначенный период. В последующем периоде базовая сумма изменяется на эту величину процента, таким образом достигается прогрессивное или лавинообразное увеличение суммы средств. При подсчете по формуле простого процента, базовая сумма всегда остается неизменной.
https://www.youtube.com/watch?v=EEWnFs6Nu10
Сложный процент — это процент начисленный на процент
Вся эта теория для неподготовленного читателя кажется через чур трудоемкой и запутанной. Но мы вас уверяем, ничего сверхсложного в формуле сложного процента и его отличия от простого нет. Сейчас разберем несколько задач и все встанет на свои места.
Примеры расчета простого и сложного процента
Формула простых и сложных процентов на малом периоде имеет незначительную разницу. Рассмотрим примеры.
Простой
Вы положили на обычный депозитный счет 1000 рублей под 10% годовых на 3 года. Через 3 года вы снимаете 1300 рублей. Так работает простой процент.
Сложный
Вы положили на депозитный счет 1000 рублей, но в характеристиках вклада указано «с ежегодной капитализацией процентов». Те же — 10% годовых, срок тот же — 3 года. Через 3 года вы снимаете уже 1331 рубль. За счет эффекта сложного процента вы получили больше на 31 рубль, чем в первом случае.
Как начинающему инвестору получить высокую доходность? Как вкладывать в самые надежные инструменты в стране? Смотрите бесплатный вебинар «Первый шаг от депозитов к инвестированию»
Подробнее о сложном проценте
Простые проценты нам больше не интересны, а формула сложного выглядит так:
S — сумма, которую вы снимете в конце n — временной период (может быть как в годах, так и в месяцах)
Давайте теперь посчитаем на суммах и процентах более приближенных к реальности, чтобы ощутить разницу в полной мере.
Задача №1
Дано:
- банковский депозит на сумму 100 тыс. руб.
- процентная ставка 8% годовых
- срок 4 года
- присутствует ежегодная капитализация процентов
Нужно найти:
- конечную результирующую сумму (доход + %)
В данном случае происходит ежегодная капитализация процента по вкладу. В некоторых банках также бывает услуга ежемесячной капитализации процентов. Об этом в задаче ниже.
Задача №2
Дано:
- банковский депозит на сумму 100 тыс руб.
- процентная ставка 8% годовых
- период 4 года
- ежемесячная капитализация
Нужно найти:
- конечную результирующую сумму (доход + %)
В формуле нужно применять ежемесячный процент, для этого 8 разделим на 12 месяцев. Получается 0,67% — это процент за месяц. И обратите внимание, степень теперь равна 48 — это количество месяцев за 4 года. Подставляем его в формулу:
Выводы
При ежемесячной капитализации результирующий доход вкладчика получился больше на 1736 рублей.
Чтобы сложный процент работал, не нужно снимать начисленные проценты, пусть они капитализируются на счете. Тогда вы получите больше выгоды от депозита.
Пример расчета с реальным банковским вкладом
Выше мы рассмотрели упрощенные примеры работы сложного процента. На самом деле банки используют немного усложненную формулу.
Ставка процентов представляется как
g — ставка в % годовых, разделенная на 100. Если 8% годовых, то получаем g=0,08
d — количество дней, через которое проценты капитализируются с базовой суммой
y — кол-во дней в году
Формула универсальная и позволяет сделать вычисление для разных типов депозитов. Таким образом, наша основная формула стала чуть-чуть сложнее:
Математическое понятие «геометрическая прогрессия» помогает работать банковскому вкладу с капитализацией гораздо более эффективно, чем без капитализации. Человеческий мозг не всегда может представить разницу или она поначалу ему кажется не существенной. В действительности, на значительных отрезках времени сложный процент начинает играть огромную роль при построении капитала.
Пример расчета на большом отрезке времени
Возьмем одновременно 2 примера с простым и сложным процентами, чтобы разница была наглядной. В обоих вариантах начальная базовая сумма будет составлять 10 тыс. руб. на 20 лет под 10% годовых. В столбцах «сложный процент» сумма процентов каждый год будет прибавляться к базовой сумме.
https://www.youtube.com/watch?v=sFStiPDvw8c
Как мы видим при длительном отрезке капитализация процентов выглядит очень поразительным инструментом! И чем больше период вложений, тем более разительной становится разница. Но давайте рассмотрим еще более впечатляющий пример.
Как поможет сложный процент в построении капитала?
Самый впечатляющий пример работы сложного процента будет ниже.
Представьте, что базовая сумма у вас совсем мизерная — 1000 рублей. Но вы каждый месяц можете откладывать от зарплаты по 1000 рублей.
Теперь прикинем варианты, какие проценты дают доступные средства сохранения и инвестирования денег в год:
- 5% — государственные облигации, так называемые облигации федерального займа. Это упрощенно, на самом деле суммы может быть побольше.
- 10% — самый щедрый банковский вклад
- 15% — смешанный инвестиционный портфель акций и облигаций
- 20% — такой процент годовых может дать портфель из акций фондовой биржи.
Давайте не будем больше приводить формулы, так как мы уже все подробно рассказали. Теперь просто возьмем итоговые цифры, которые поражают воображение неподготовленного человека.
Как мы видим результаты впечатляющие, суммы растут как снежный ком. Вы все можете проверить по калькулятору или экселю, здесь нет обмана. Вы действительно можете стать миллионером, откладывая всего по 1000 рублей в месяц.
А что если вы сможете откладывать по 10000 рублей? Теперь подрисуйте в таблице везде по нолику и еще раз удивитесь результатам.
Вы можете возразить, что действительно интересные суммы появляются только при 20% годовых. А вкладывать в акции вы, мол, не умеете. В действительности, это не такое сложное занятие. Для этого наш сайт real-investment.net и создан. Есть очень простые стратегии инвестирования в акции. Вам не понадобится думать, как выбирать акции и каждый день или неделю продавать их или покупать.
Тут все почти как с банковским вкладом. Вы просто откладываете деньги покупаете на них каждый месяц одни и те же акции или паи фонда. Это краткая суть стратегии.
Почему в акции инвестировать безопасно? Почему акции непременно будут расти на 20% годовых? Подробная информация о стратегии и ответы на эти вопросы вы получите на нашем вебинаре об индексном инвестировании, а точнее записи этого вебинара.
Подробнее о том, как купить акции частному лицу
Вспомогательные формулы
Привожу еще пару вспомогательных формул, которые могут пригодиться при составлении личного финансового плана. Они выражаются из уже написанных выше. Рассмотрим все на примерах задач.
Заключение
Описанные формулы простых и сложных процентов построения капитала активно используются во всем мире, будь то обычное накопление или инвестирование. Профессиональные финансовые советники и богатейшие люди мира одинаково хорошо отзываются и рекомендуют прибегать к сложным процентам для улучшения своего финансового положения.
Как мы увидели, не обязательно иметь крупную сумму в самом начале, главное регулярно откладывать деньги и пользоваться хорошим процентом.
Видео:Простые и сложные процентыСкачать

Простые и сложные проценты
Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени.
Проценты различаются по базе их начисления. Применяется постоянная или последовательно изменяющаяся база для расчета. В последнем случае за базу применяется сумма, полученная на предыдущем этапе наращения или дисконтирования, т.е. проценты начисляются на проценты. При постоянной базе используют простые, при измененной — сложные процентные ставки.
Под наращенной суммой ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока.
Наращение по простой процентной ставке:
, (1)
где S – наращенная сумма; P – первоначальная сумма, n – срок, r – ставка наращения (десятичная дробь).
Наращение по сложной процентной ставке:
, (2)
где j — сложная процентная ставка; n — число лет наращения, m – число начислений процентов в году.
https://www.youtube.com/watch?v=er84ZZ_ryHM
Номинальная ставка – это годовая ставка сложных процентов при одноразовом начислении процентов в году по ставке j.
Эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов в году по ставке .
Наращение по непрерывной процентной ставке:
При непрерывном наращении процентов применяют особый вид процентной ставки — силу роста ( ). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.
, (3)
Дисконтирование и учет по простым процентным ставкам
Термин дисконтирование употребляется как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени.
В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n , необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например при разработке условий контракта.
Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды.
В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называется учетом, а удержанные проценты — дисконтом.
В зависимости от вида процентной ставки применяют два метода дисконтирования — математическое дисконтирование и банковский (коммерческий) учет. В первом случае используется ставка наращения, во втором — учетная ставка.
Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды.
, (4)
Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой).
Получив при наступлении срока векселя деньги, банк реализует дисконт. При учете векселя применяется банковский или коммерческий учет, согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока.
При этом применяется учетная ставка d.
, (5)
Для ставки наращения прямой задачей является определение наращенной суммы, обратной – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении .
Ставка Прямая задача Обратная задача
r (6)
d .
Учетная ставка отражает фактор времени более жестко. Например, при d = 20 % уже 5-ти летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете.
Определение срока ссуды и величины простой процентной ставки
Продолжительность срока ссуды в годах получим, решив уравнения (1) и (5) относительно n:
, (7) , (8)
По этим же уравнениям можно определить и процентные ставки:
, (9) , (10)
Определение срока платежа и сложных процентных ставок
Продолжительность срока платежа в годах получим, решив уравнения (2) относительно n:
, (11)
Поэтому же уравнению можно определить и сложную процентную ставку:
, (12)
Продолжительность срока платежа в годах при наращении по постоянной силе роста и по изменяющейся с постоянным темпом силе роста получим, решив уравнения (3) относительно n:
, (13)
Поэтому же уравнению можно определить и силе роста :
, (14)
Потоки платежей. Постоянные финансовые ренты
Погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. – называют потоки платежей.
Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке платежей членами являются как положительные (поступления), так и отрицательные величины (выплаты), а соответствующие платежи могут производиться через разные интервалы времени.
https://www.youtube.com/watch?v=DKyj6qRj9U8
Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой или просто рентой.
Рента характеризуется следующими параметрами: член ренты — размер отдельного платежа, период ренты – временной интервал между двумя последовательными платежами, срок ренты – время от начала первого периода ренты до конца последнего периода, процентная ставка.
По количеству выплат членов ренты на протяжении года, ренты делятся на годовые, P — срочные (P – количество выплат в году), непрерывные (много раз в году).
Обобщенные параметры потоков платежей
Анализ потока платежей предполагает расчет одной из двух обобщающих характеристик: наращенной суммы или современной стоимости.
Наращенная сумма –сумма всех членов потока платежей с начисленными на них к концу срока процентами.
Современная стоимость потока платежей – сумма всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени.
Допустим, имеется ряд платежей , выплачиваемых спустя время после некоторого начального момента времени, общий срок выплат n лет. Необходимо определить наращенную на конец срока сумму потока платежей, если проценты начисляются раз в году по сложной ставке j, то:
, (15)
Как видим, наращенную сумму в заданных условиях получают методом прямого счета. Современную стоимость такого потока найдем прямым счетом – как сумму дисконтированных платежей. Обозначив эту величину, как A, получим:
, (16)
где — дисконтный множитель по ставке j.
Между величинами A и S существует функциональная зависимость:
(17)
Очень важным является различие рент по моменту выплат платежей в пределах периода. Если платежи осуществляются в конце периодов, то такие ренты называют обыкновенными или постнумерандо, если же платежи производятся в начале периодов, то их называют пренумерандо.
Годовая рента
В течении n лет в банк в конце каждого года вносится по R руб. На взносы начисляются сложные проценты по ставке % годовых. Все члены ренты, кроме последнего, приносят проценты – на первый член ренты начисляются (n-1) раз, на второй (n-2) и т.д.
.
Если переписать этот ряд в обратном порядке, то получим геометрическую прогрессию со знаменателем (1+ j ) и первым членом R.
, (18)
При начислении процентов m раз в году то:
; (19)
Если платежи осуществляются в начале периодов то
; (20)
При начислении процентов m раз в году то:
; (21)
Современная стоимость постоянной ренты постнумерандо
, (22)
Множитель, на который умножается R, называется коэффициентом приведения ренты и обозначается :
При , (23)
В этом случае: , (24)
При дисконтировании m раз в году:
, (25)
Определение срока ренты
P = 1
m = 1
p = 1
m > 1
P > 1
m = 1
m = p
m¹p
При расчете срока ренты необходимо принять во внимание следующие моменты:
1. Расчетные значения срока будут дробные. Для годовой ренты в качестве n удобнее принять меньшее ближайшее число. У p-срочной ренты результат округляется до ближайшего целого числа периодов.
2. Если округление производится до меньшего целого числа, то наращенная сумма или современная стоимость ренты оказывается меньше заданной. Возникает необходимость в соответствующей компенсации.
Например, если речь идет о погашении задолженности путем выплаты постоянной ренты, то компенсация может быть осуществлена соответствующими платежом в начале или конце срока или с повышением суммы члена ренты.
💡 Видео
Формула сложного процентаСкачать

Алгебра 10 класс (Урок№4 - Прогрессии и сложные проценты.)Скачать

Простые и сложные процентыСкачать

Финансовая грамотность. Простые и сложные проценты.Скачать

Что такое сложный процент? Капитализация.Скачать

#5. СЛОЖНЫЕ ПРОЦЕНТЫСкачать

ВСД02. Простые и сложные проценты. Просто о сложном.Скачать

#4. ПРОСТЫЕ ПРОЦЕНТЫСкачать

Сложные проценты.Скачать

Проценты. Как считать проценты? | МатематикаСкачать

Простые и сложные процентыСкачать

9 класс. Формула сложных процентовСкачать

ЕГЭ по математике - Сложные процентыСкачать

Сложный процент понятным языком. Магия сложного процента.Скачать

ВСД03. Простые и сложные проценты. Внутригодовые начисления!Скачать